
Welcome to the Robertson-Anderson Lab!
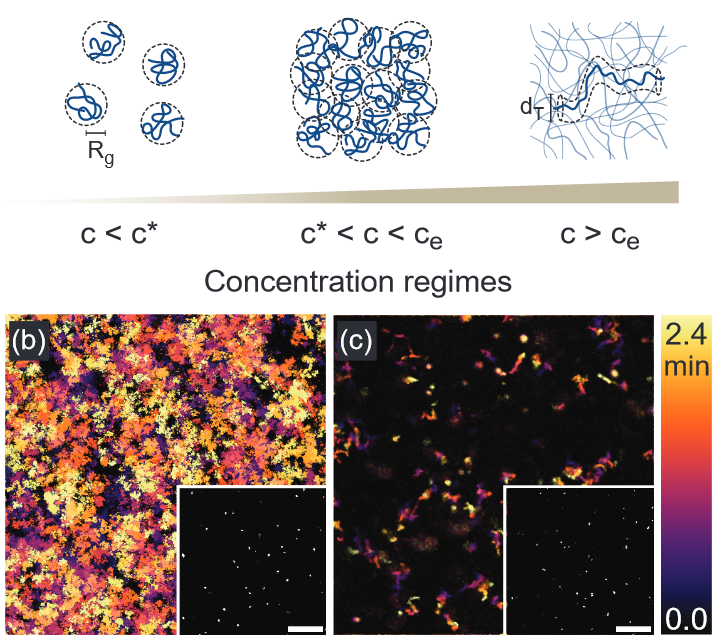
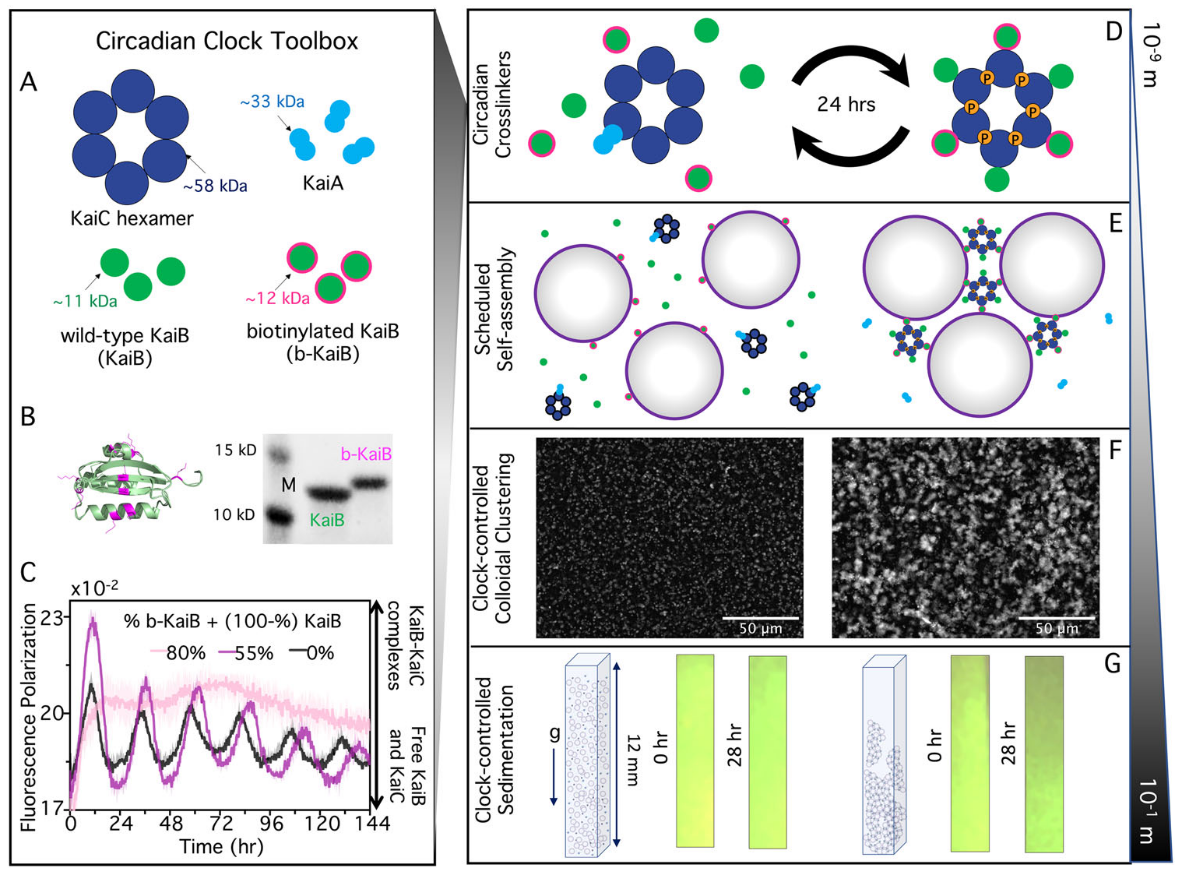
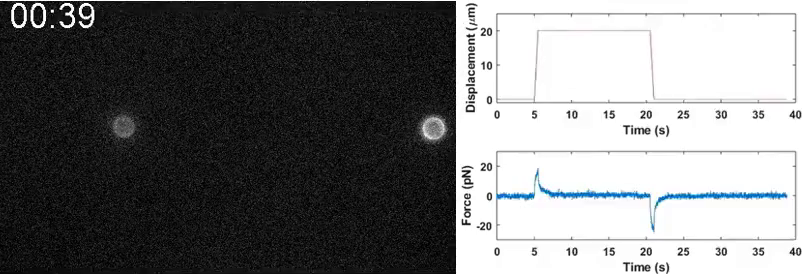
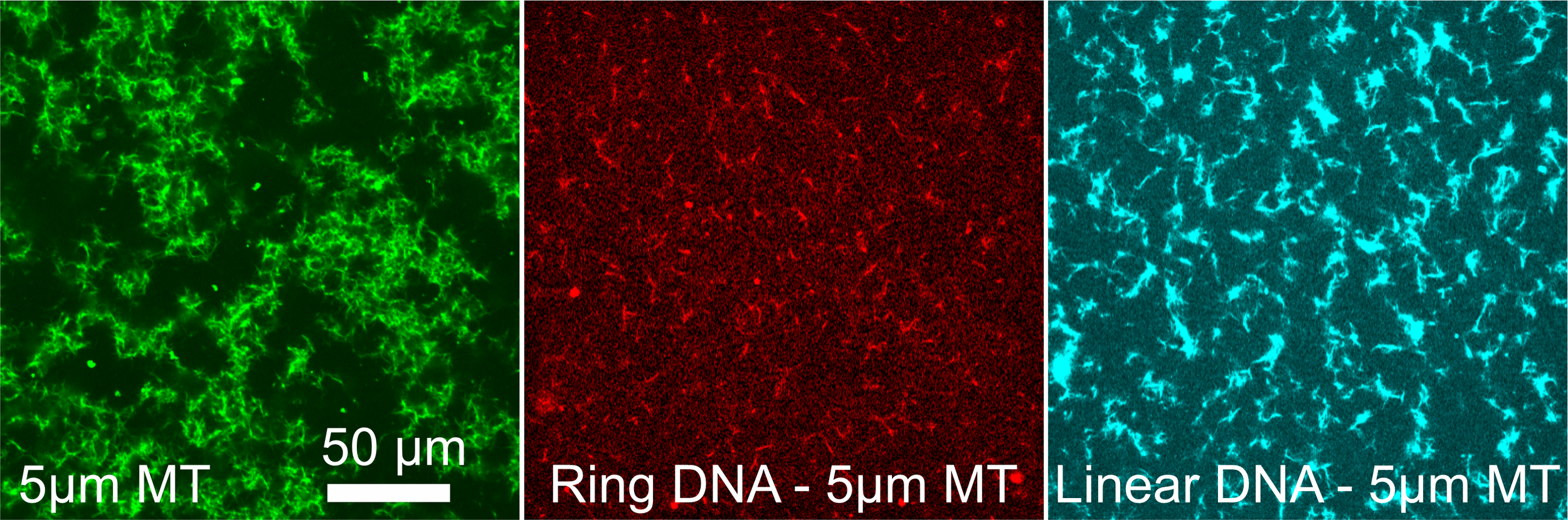
Our lab seeks to elucidate the microscale mechanics and macromolecular dynamics in bio-inspired soft and active matter systems and biopolymer networks. We engineer and use novel optical tweezers microrheology and fluorescence microscopy techniques to probe these systems across broad spatiotemporal scales and from steady-state to far from equilibrium. Inspired by the complexity of biological cells and fluids, we also design entangled, crowded, heterogeneous, topologically-distinct, and non-equilibrium biopolymer composites to address critical questions in soft matter, active matter, and polymer physics.