INFORMATION AND ANALYSIS

1. Measures of central tendency

a. Mean (arithmetic mean)

Population:

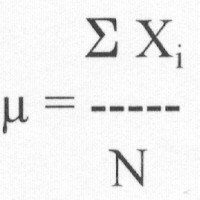
Sample:

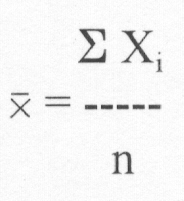
Ex. - Yen / $

AVERAGE function in Excel: =AVERAGE(data range)

.

.

b. Median

Value where half of observations are above, half below

(1) Odd number of observations

Use middle value

Ex. - Yen / $

MEDIAN function in Excel: =MEDIAN(data range)

.

.

(2) Even number of observations

Use average of the middle pair

Ex. - Yen / $

.

.

c. Mode

Value that occurs most frequently

Ex. - Yen / $

MODE function in Excel: =MODE(data range)

.

.

d. Geometric mean

Measures rate of change of a variable over time

(1) n^th root of the product of n values

X_G = (X₁ * X₂ * . . . * X_n) ^1/n

(2) Geometric mean rate of return

R_G = [(1 + R₁) * (1 + R₂) * . . . * (1 + R_n)] ^1/n - 1

Ex. -

.

.

.

2. Measures of variation

.

.

.

.

.

.

a. Range

Maximum - minimum

Ex. - Yen / $

Take difference of MIN and MAX functions of Excel: =MAX(data range) - =MIN(data range)

.

.

b. Interquartile range

(1) Definitions

First quartile (Q1) = 25% of observations smaller, 75% larger

Second Quartile (Q2) = 50% of observations smaller, 50% larger

Third quartile (Q3) = 75% of observations smaller, 25% larger

(2) Calculation

Q1 = (n + 1) / 4 th ordered observation

Q2 = 2*(n+1) / 4 th ordered observation

Q3 = 3*(n+1) / 4 th ordered observation

Ex. - Yen / $

.

.

.

.

IQR = Q3 - Q1

Ex. - Yen / $

.

.

c. Variance and standard deviation

(1) Population

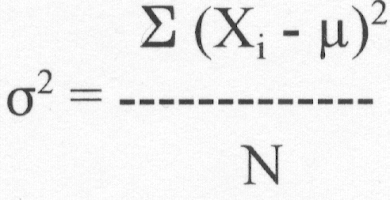
Ex. - Yen / $

Population variance in Excel: =VARP(data range)

.

.

(2) Sample

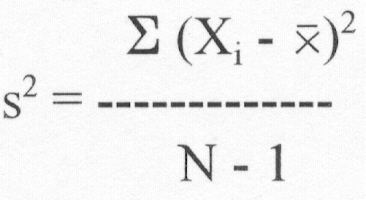
Ex. - Yen / $

Sample variance in Excel: =VAR(data range)

.

.

(3) Standard deviation

.

.

Ex. - Yen / $

Population standard deviation in Excel: =STDEVP(data range)

Sample standard deviation in Excel: =STDEV(data range)

.

.

 

Mutual Fund Risk Measures

All measures given in the Descriptive Statistics function of Excel: Tools | Data Analysis | Descriptive Statistics

.

.

d. Coefficient of variation (CV)

CV = (S / X) * 100%

Used to compare variation when data measured in different units or vary significantly in magnitude

Ex. - Stock prices

.

.

.

.

3. Shape

a. Characterization

(1) Symmetric or zero-skewness

.

.

.

.

.

(2) Right-skewed or positive skewness

.

.

.

.

.

(3) Left-skewed or negative skewness

.

.

.

.

.

b. Evaluation

(1) Mean vs. median

• Mean = median => symmetric

• Mean > median => right skewness

• Mean < median => left skewness

Ex. - Yen / $

.

.

.

.

(2) Five number summary

Minimum, Q1, median, Q3, maximum

(a) Evaluation

i. Symmetric

• MInimum -> median = median -> maximum

• Minimum -> Q1 = Q3 -> maximum

ii. Right-skewed

• Median -> maximum > minimum -> median

• Q3 -> maximum > minimum -> Q1

iii. Left-skewed

• Minimum -> median > median -> maximum

• Q3 -> maximum < minimum -> Q1

Ex. - Yen / $

.

.

.

.

(b) Box-and-whisker plot - plot of the five-number summary

.

.

.

.

.

.

.

.

.

.

.

.

4. Ethical issues

• Good and bad results should be documented

• Results should be presented in an objective manner

• Need to choose appropriate summary measures

• Intent is key again