RC Circuits

If the voltage applied to a series combination of a capacitor and resistor is suddenly changed, the charge on the capacitor will gradually change as the voltage of the capacitor gradually adjusts to the new situation. When steady state is reached, the new voltage across the capacitor again equals the voltage applied to the resistor -capacitor series combination. As the charge is changing there is a current i, flowing through the resistor, thus there is a voltage across the resistor for some time. The charge and voltage on the capacitor move toward their new equilibrium values exponentially, with a time constant given by $\tau = RC$. It can be shown that, if the capacitor is charging up, then the voltage across it is given by

$$V_c = V_o (1 - e^{-t/\tau}),$$

whereas if it is discharging, its voltage is

$$V_c = V_o e^{-t/\tau}.$$

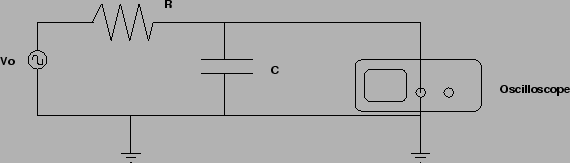
Obtain a capacitance from the bins and estimate the capacitance of the capacitor by measuring the RC time constant. How? Well, with an oscilloscope of course. Putting aside the question of how to use such a thing, let's focus on the RC time constant. First, show that whether charging or discharging, the time necessary for the voltage to drop to 1/2 of its initial value, or rise to 1/2 of its final value, is just

$$t_{1/2} = \tau \ln{2}.$$

Using the oscilloscope, measure the so called half life of the charging and discharging signal and from it compute the capacitance of your chosen capacitance. Do this by connecting the vertical input of the oscilloscope in parallel with the capacitor, so that you can observe and measure the voltage across the capacitor, as shown in the figure below. Oh, I forgot: use one of the (known) resistors from the previous part of the lab.