Introduction:

According to Faraday's law of induction, the EMF, E, induced in a coil of N turns is

$$E = - N \frac{d \Phi}{dt} = - N \lim_{\Delta t \rightarrow 0} \frac{\Delta \Phi}{\Delta t }$$ (1)

where

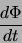$$\frac{d \Phi}{dt}$$ (2)

is the rate of change of magnetic flux in the coil. The flux $\Phi$ is given by

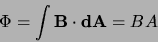$$\Phi = \int \vec{B} \cdot \vec{dA} = BA$$ (3)

where the second equality is true whenever the magnetic field is the same everywhere, or is at least constant over the region of interest, and parallel to the surface normal vector.

In this experiment we will see how Faraday's idea works out in the case of a time changing magnetic field in the vicinity of a primary coil. Consider two concentric solenoids, one placed inside of the other like so:

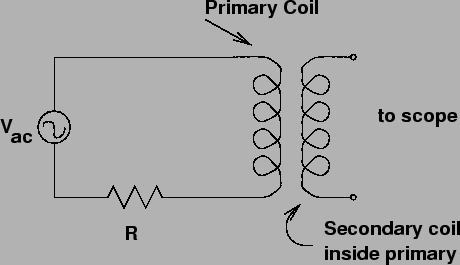
The secondary coil is placed inside the primary coil. Even though there is no conducting link between the circuit that the primary coil is in, this circuit will drive a current through a secondary coil! How can it do that? Well, by producing a time changing magnetic flux through the secondary coil. A time varying current (produced by a function generator) is passed through the primary coil, thus creating a fairly uniform time varying magnetic field down the bore of the primary coil. The time dependence of the current is given by

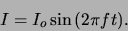$$I = I_{o} \sin{(2\pi ft)}.$$ (4)

One can calculate the magnitude of the time changing magnetic field using this current. A portion of the magnetic flux created by primary coil ``links'', or passes through, the secondary coil. Since the flux is changing in time, we expect a voltage to be induced across the secondary coil, according to Faraday's Law. Once the time rate of change of the magnetic flux is calculated, one can easily calculated the expected induced EMF across the secondary coil. Simply measure the induced EMF with the oscilloscope, and compare your calculated value with your experimental value.