Procedure:

Experiment A - Simple Converging Lenses and the Microscope:

1. For this experiment, you shall require two portly little lenses, bulging at the middle (small focal length) sort of lenses. Measure the focal length of the 2 lenses.How to do this? That's easy: find an object at infinity, and focus on it, marking the distance between the lens and the focal plane. If the object is at infinity, the focal length coincides with the image distance. Show that the Gaussian lens formula predicts this. Use your ingenuity in finding such an object. Relatively infinite, I suppose, will have to do. What do you suppose that means? Relative to what? Commit your thoughts to your lab book, and make a measurement. Actually, an object at infinity is not required, any old distance will do provided one can accurately measure the object and image positions!
2. Place the light source at about 3 fo/2 from the objective lens and locate its image. Perform a simple calculation to predict where the image should form. Mark the difference and see ``what gives'', that is, make sure of all positions. Use the clear plastic real image viewers for this task.

3. Once you have completed this task, replace the light source with the graph paper, making very certain that they occupy the same positions.
4. Place the eyepiece lens on the bench somewhat past the image position of objective so as to form a virtual image of the objective's image.
5. Adjust the position of the eyepiece lens until there is no parallax between the image and the lined paper viewed directly (with the other eye). Start with the eye piece rather too close to the objective so that the parallax is obvious for gentle side to side head motions. One has to defocus the eye looking at the image so that both the image and the object are, at once, clearly (ha!) in view. Sound difficult? You Bethcha! Gradually, move the eye piece out until the parallax goes away. It is subtle, and will likely drive you crazy. Let me put it this way: extra credit for those that actually persevere to find the ``no parallax position''. The lined paper and the final image are now equidistant.
6. By comparing lines measure the experimental magnification.

7. Calculate the expected magnifying power from the formula 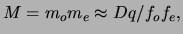$M =m_o m_e\approx Dq/f_{o}f_{e},$ where q is the distance between the focal point of the objective lens, and the image that it forms. This is the lateral magnification of the objective multiplied by the magnifying power of the eye piece, which ought to be exactly what we measure experimentally (the angular magnification) if the image plane coincides with the object plane. Ah, and now the reason for the ``no parallax'' position comes into focus. Compare to the experimental results in (5).

   

Experiment B - Telescope:

1. Do step 1 from Experiment A. Here one needs a very long focal length objective and a small focal length eye piece.
2. Place the light source far, far away from the optics bench, and find its image. You will need to affix a piece of grid paper there so be 'ware. Is the image exactly where it is supposed to be? Make measurements to find out.
3. Place the eyepiece lens just past the objective's image and find observe the virtual image formed by the eyepiece.
4. Adjust the eyepiece until the final image has no parallax with the distant grid. Follow the notes from Experiment A (part 4).
5. Measure the magnification. This is the experimental magnifying power of the telescope. Record your experimental uncertainty of the this magnification.

6. The expected magnifying power of the telescope can be shown to be M f_of_e Calculate M and compare to your experimental value.

Note: Extra credit will be given to any student who can see straight after the experiment is complete.