Part A - Charging and Discharging a Capacitor:

If the voltage applied to a series combination of a capacitor and resistor is suddenly changed, the charge on the capacitor will gradually change as the voltage of the capacitor gradually adjusts to the new situation. When steady state is reached, the new voltage across the capacitor again equals the voltage applied to the resistor -capacitor series combination. 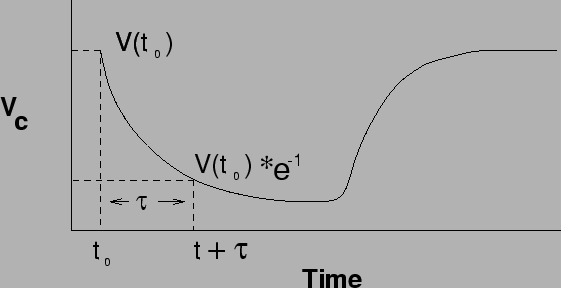As the charge is changing there is a current i, flowing through the resistor, thus there is a voltage across the resistor for some time. The charge and voltage on the capacitor move toward their new equilibrium values exponentially, with a time constant given by $\tau = RC$.

Obtain the value of the resistance and capacitance, and calculate the expected $\tau$. Compare this with the experimental value as described below.

Connect the oscillator, the resistance box and the capacitance box in a single, series loop. Set the oscillator for square-wave output, set the resistor for 5000 ohms and the capacitor for .01 microfarads. Check the oscillator ground-side output that it is connected to the capacitor and the scope ground.

Connect the vertical input of the oscilloscope in parallel with the capacitor, so that you can observe and measure the voltage across the capacitor. Observe the capacitor voltage at a low frequency. You should see that the capacitor voltage appears to be approximately a square wave. Also observe the capacitor voltage when the square-wave frequency is much higher than the reciprocal of the RC time constant. You should observe approximately a ``triangle-wave" voltage on the capacitor.

Measure the time constant at an intermediate frequency, when the square-wave period is about 3-5 times the RC time constant. The time constant can be determined as in the figure below.