



Next: Part C - RLC
Up: Procedure:
Previous: Part A - Charging
Contents
If a sine-wave AC voltage is applied to a series RC circuit,
Ohm's law becomes V = IZ, where Z is the series impedance
produced by the resistance R in series with the capacitive
reactance of the capacitor,
 . The total impedance Z
is given by
. The total impedance Z
is given by
The impedance looks like the vector sum of two impedances, the
hypotenuse of a right triangle whose base is 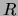 and whose altitude is
and whose altitude is
 . What is the significance of the angle between the hypotenuse
and the base? Yes! It is the phase angle between the current and the
voltage. Calculate the frequency at which this angle should be
. What is the significance of the angle between the hypotenuse
and the base? Yes! It is the phase angle between the current and the
voltage. Calculate the frequency at which this angle should be
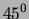 , set the function generator to that frequency, and measure the
phase difference. Then, measure the voltage amplitudes of the source,
the resistor, and capacitor, and check to see if these add like
vectors. Recall that Kirchhoff's voltage loop rule says that the
voltages around a loop add like scalars.
, set the function generator to that frequency, and measure the
phase difference. Then, measure the voltage amplitudes of the source,
the resistor, and capacitor, and check to see if these add like
vectors. Recall that Kirchhoff's voltage loop rule says that the
voltages around a loop add like scalars.




Next: Part C - RLC
Up: Procedure:
Previous: Part A - Charging
Contents
greg severn
2000-10-24
![]() . The total impedance Z
is given by
. The total impedance Z
is given by