



Next: Questions
Up: WAVE PROPERTIES OF LIGHT
Previous: Introduction:
Contents
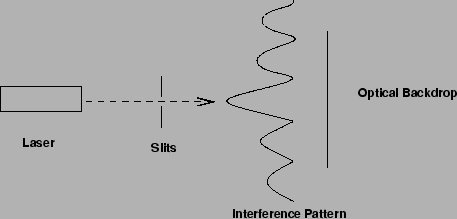
Single slit experiment:
The single slit diffraction pattern should have minima at
(_min) = n (a) for n =
1,2,...
where 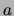 is the slit width, and
is the slit width, and 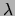 is the given
wavelength of the laser light.
is the given
wavelength of the laser light.
- Observe the single slit diffraction pattern, and make the
necessary measurements to determine the angles associated with minima. Be very careful to make the distance to the
optical
backdrop long enough to make measurements of the minima and maxima
easy to do.
- Use the traveling microscope to measure the width of the
slits, and thus experimentally determine the wavelength of
the light.
Double slit experiment:
If light is a wave, an interference pattern should be created, and if we are lucky, it will even be visible, much like that
observed in the single slit experiment with this difference: there are
minima within the maxima.
The maximum should appear at angles
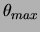 where
d (_max) = m for m = 0,1,2,...
and the minima should appear at
d (_min) = ( m + 12 ) for
m = 0,1,2,...
where
where
d (_max) = m for m = 0,1,2,...
and the minima should appear at
d (_min) = ( m + 12 ) for
m = 0,1,2,...
where 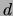 is the distance between the slits.
is the distance between the slits.
- Observe the double slit interference pattern, and make
the necessary measurements and thus determine angles
associated with the maxima and minima.
- Use the traveling microscope to measure the distance
between the slits and thus determine the wavelength of the
light.
Multiple slit experiment:
A diffraction grating consists of a regular array of slits
or bars with equal spacing. The condition for maxima is
the same as for a double slit.
Observe the pattern produced by the diffraction grating and record the measurements necessary for calculating the angle of the first diffraction maximum.
From the number of lines per inch, deduce the wavelength of the laser light.




Next: Questions
Up: WAVE PROPERTIES OF LIGHT
Previous: Introduction:
Contents
greg severn
2000-10-24


![]() is the slit width, and
is the slit width, and ![]() is the given
wavelength of the laser light.
is the given
wavelength of the laser light.
![]() where
d (_max) = m for m = 0,1,2,...
and the minima should appear at
d (_min) = ( m + 12 ) for
m = 0,1,2,...
where
where
d (_max) = m for m = 0,1,2,...
and the minima should appear at
d (_min) = ( m + 12 ) for
m = 0,1,2,...
where ![]() is the distance between the slits.
is the distance between the slits.